En marketing, on appelle typologie un traitement de données qui vise à régrouper des individus en fonction de leur proximité/ressemblance sur un ensemble de variables. En terme d’analyse statistique, on va utiliser une analyse factorielle de type « ACM » (= Analyse des Correspondances Multiples) suivie d’une classification ascendante hiérarchique (« CAH »).
Nous allons donc voir comment faire cela avec R.
+ Chargement des données :
|
1 |
M <- read.csv("data_typo.csv", header = TRUE, sep = ";") |
> Type du fichier d’exemple : CSV, séparateur « point-virgule », questions de type qualitatif et questions à choix multiples au format dichotomique (1 = « Cité » / 0 = « Non Cité »)
+ Visualiser le nom des variables/en-têtes de colonnes :
|
1 |
colnames(M) |
+ Gestion des valeurs manquantes NA :
|
1 2 3 4 5 6 |
vm <- which(is.na(M$q1)) # sélectionner les individus ayant une valeur manquante à la question "q1" par exemple vm <- which(is.na(M[, 3])) # autre écriture si, par exemple, la question "q1" est en colonne 3 dans les données # vm contient la liste des numéros de lignes correspondant aux individus ayant une valeur manquante (NA) pour "q1" M <- M[-vm, ] # exclusion des NA de q1 dans le jeu de données global |
+ Sélection d’individus d’après un filtre :
|
1 2 3 4 5 6 7 8 |
ut <- which(M$util == 1) # ex : on ne veut réaliser l'analyse que sur les profils "utilisateurs", i.e. les gens ayant choisi la modalité 1 à la question "util" # ou ut <- which(M[, 1] == 1) # si la question "util" est en 1ère colonne dans les données # ut contient la liste des numéros de lignes correspondant aux individus "utilisateurs" M <- M[ut, ] # selection des profils "utilisateurs" parmis le jeu de données global |
+ Sélection des variables typo :
Un certain nombre de variables ont été retenues pour réaliser la typologie. On va donc récupérer les données correspondant à ces variables en particulier.
|
1 |
list_vars <- c(3:5, 12, 24:27) # contient les numéros des colonnes correspondant aux variables choisies pour la typo |
> Au final, « list_vars » contient les numéros suivants : 3, 4, 5, 12, 24, 25, 26 et 27
|
1 |
X <- M[, list_vars] |
> La matrice « X » va contenir uniquement les variables (actives et illustratives) qui serviront dans la typologie (dans notre exemple : 8 variables).
+ Vecteur de poids :
Dans le cas où il existe une pondération sur les individus, on va avoir besoin d’un vecteur contenant ces poids.
|
1 |
poids <- M$poids |
- Analyse des Correspondances Multiples -
+ Type des variables = « factor » :
Dans R, il va falloir spécifier que les variables utilisées pour notre analyse sont de type « qualitatif » (ie. avec un nombre fini de modalités entières) : il s’agit de mettre les variables de « X » au format « factor ».
|
1 2 3 |
X <- apply(X, 2, as.factor) str(X) # l'appel à la fonction "str" va nous permettre de vérifier que toutes les variables ont bien le type "factor" souhaité |
+ ACM :
|
1 2 3 |
library(FactoMineR) # va permettre de charger la librairie contenant la fonction permettant de réaliser l'ACM acm <- MCA(X, ncp = 80, graph = FALSE, quali.sup = c(7, 8), row.w = poids) # réalisation de l'ACM |
Syntaxe : Arguments de la fonction « MCA »
| X | matrice des variables actives et illustratives utilisées pour l’ACM |
| ncp | nombre de composantes retenues au maximum |
| graph = FALSE | empêche l’affichage de sorties graphiques (TRUE pour l’autoriser) |
| quali.sup = c(…) | quali.sup = vecteur des numéros de colonnes dans X qui correspondent aux variables illustratives (existe aussi « quanti.sup ») |
| row.w = poids | permet de spécifier le vecteur des poids des individus (si pas de pondération, ne pas mettre cet argument) |
+ Sélection des composantes :
On va sélectionner un nombre de composantes permettant d’obtenir le maximum d’informations (par exemple 80%).
|
1 2 3 |
vp <- acm$eig$eigenvalue # vecteur des valeurs propres associées aux composantes de l'ACM 100*(cumsum(vp)/sum(vp)) # pourcentage cumulé d'info apportée par les composantes de l'ACM |
> On va ensuite sauvegarder les composantes retenues (ainsi que les données initiales) dans un fichier csv :
|
1 2 3 4 5 6 7 |
IC <- acm$ind$coord[, 1:25] # ici on a retenu 25 composantes colnames(IC) <- paste0("Dim.", 1:25) C <- cbind(M, IC) write.csv(C, file = "data_total_with_acm_coord.csv", row.names = FALSE, quote = FALSE) |
- Classification -
On va maintenant réaliser une classification sur les composantes de l’ACM que nous avons retenues afin de séparer nos individus en plusieurs groupes.
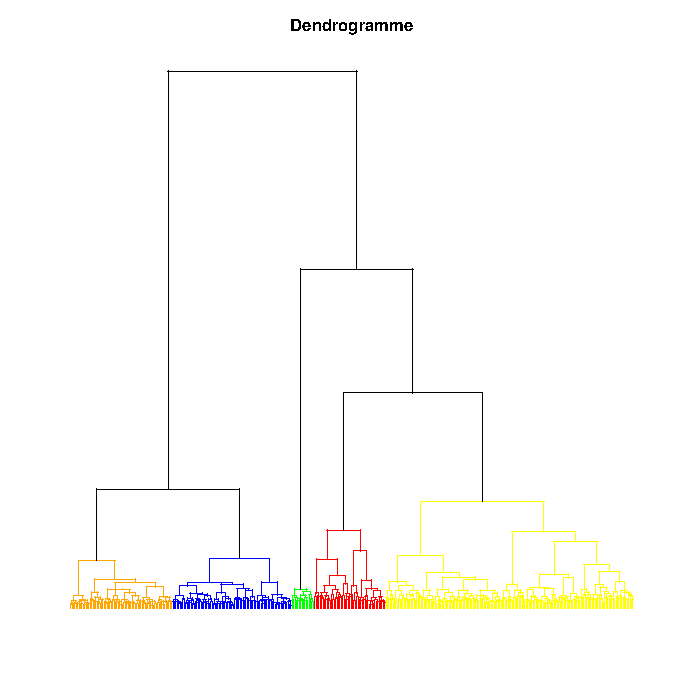
+ Dendrogramme :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
dendro <- hclust(dist(model.matrix(~-1+Dim.1+Dim.2+Dim.3+Dim.4+Dim.5+Dim.6+Dim.7+Dim.8+Dim.9+Dim.10+Dim.11+Dim.12+Dim.13+Dim.14+Dim.15+Dim.16+Dim.17+Dim.18+Dim.19+Dim.20+Dim.21+Dim.22+Dim.23+Dim.24+Dim.25,C)), method = "ward") plot(dendro) # représentation de l'arbre de classification # ou : représentation plus personnalisée de l'arbre de classification (nécessite une connexion internet) source("http://addictedtor.free.fr/packages/A2R/lastVersion/R/A2R") pdf("dendro5.pdf") # va permettre de sauvegarder le dendrogramme au format pdf A2Rplot(dendro, k = 5, lty.up = 1, lty.down = 1, boxes = FALSE, col.down = c("orange", "blue", "green", "red", "yellow"), lwd.down = 1, col.up = "black", show.labels = FALSE, main = "Dendrogramme") # ici répartition en 5 groupes dev.off() |
> L’observation de l’arbre va nous permettre de décider d’un nombre k de groupes dans lesquels seront répartis les individus de l’étude.
Exemple de dendrogramme :
+ Répartition des individus dans les groupes et effectifs :
|
1 2 3 |
group5 <- cutree(dendro, k = 5) # vecteur contenant le numéro du groupe (ici entre 1 et 5) auquel appartient chaque individu table(group5) # va renvoyer le tableau d'effectifs de chacun des 5 groupes |
> On va ensuite sauvegarder les numéros de groupe des individus (ainsi que les résultats de l’ACM et les données initiales) dans un fichier csv :
|
1 2 3 |
T <- cbind(C, group5) write.csv(T, file = "data_complete_with_groups.csv", row.names = FALSE, quote = FALSE) |
- Description des groupes -
Maintenant que nous avons une répartition de nos individus en k groupes, ce qui va nous intéresser c’est de déterminer quels sont les éléments (variables) qui caractérisent ces différents groupes.
Pour cela, on peut utiliser la fonction : « catdes.w« , donc vous trouverez le code ci-dessous :
(il s’agit en fait d’une version très légèrement modifiée de la fonction « catdes » du package « FactoMineR », afin de pouvoir prendre en compte un poids sur les individus)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 |
catdes.w<-function (donnee, num.var, proba = 0.05 , weight=NULL) { lab.sauv <- lab <- colnames(donnee) quali = NULL for (i in 1:length(lab)) { lab[i] = gsub(" ", ".", lab[i]) if (is.factor(donnee[, i])) { if (levels(donnee[, i])[1] == "") { levels(donnee[, i])[1] = "NA" } if (i != num.var) { quali = c(quali, i) } } } quanti = (1:ncol(donnee))[-c(quali, num.var)] if (length(quanti) == 0) { quanti = NULL } colnames(donnee) = lab res = list() nb.modalite <- length(levels(donnee[, num.var])) nb.quali = length(quali) old.warn = options("warn") if(length(weight)==0) { weight<-rep(1,dim(donnee)[1]) } if (nb.quali > 0) { options(warn = -1) marge.li = xtabs(weight~donnee[, num.var]) nom = tri = structure(vector(mode = "list", length = nb.modalite), names = levels(donnee[, num.var])) for (i in 1:nb.quali) { Table <- xtabs(weight~donnee[, num.var] + donnee[, quali[i]]) marge.col = xtabs(weight~donnee[, quali[i]]) ML<-rowSums(Table) for (j in 1:nlevels(donnee[, num.var])) { for (k in 1:nlevels(donnee[, quali[i]])) { aux2 = Table[j, k]/ML[j] if(ML[j]==0) { aux2 = 0 } aux3 = marge.col[k]/sum(marge.col) if (aux2 > aux3) { aux4 = phyper(Table[j, k] - 1, ML[j], sum(ML) - ML[j], marge.col[k], lower.tail = FALSE) * 2 } else { aux4 = phyper(Table[j, k], ML[j], sum(ML) - ML[j], marge.col[k]) * 2 } if (aux4 < proba) { aux5 = (1 - 2 * as.integer(aux2 > aux3)) * qnorm(aux4/2) aux1 = Table[j, k]/marge.col[k] tri[[j]] = rbind(tri[[j]], c(aux1 * 100, aux2 * 100, aux3 * 100, aux4, aux5)) nom[[j]] = rbind(nom[[j]], c(levels(donnee[,quali[i]])[k], colnames(donnee)[quali[i]])) } } } } for (j in 1:nb.modalite) { if (!is.null(tri[[j]])) { oo = rev(order(tri[[j]][, 5])) tri[[j]] = tri[[j]][oo, ] nom[[j]] = nom[[j]][oo, ] if (nrow(matrix(tri[[j]], ncol = 5)) > 1) { rownames(tri[[j]]) = paste(nom[[j]][, 2], nom[[j]][,1], sep = "=") } else { tri[[j]] = matrix(tri[[j]], ncol = 5) rownames(tri[[j]]) = paste(nom[[j]][2], nom[[j]][1], sep = "=") } colnames(tri[[j]]) = c("Cla/Mod", "Mod/Cla", "Global", "p.value", "v.test") } } res$category = tri } if (!is.null(quanti)) { nom = result = structure(vector(mode = "list", length = nb.modalite), names = levels(donnee[, num.var])) for (i in 1:length(quanti)) { moy.mod = by(donnee[, quanti[i]]*weight, donnee[, num.var], mean, na.rm = TRUE) n.mod = summary(donnee[, num.var]) sd.mod = by(donnee[, quanti[i]]*weight, donnee[, num.var], sd, na.rm = TRUE) sd.mod = sd.mod * sqrt((n.mod - rep(1, nb.modalite))/n.mod) moy = mean(donnee[, quanti[i]]*weight, na.rm = TRUE) et = sd(donnee[, quanti[i]]*weight, na.rm = TRUE) * sqrt(1 - 1/sum(n.mod)) for (j in 1:nb.modalite) { v.test = (moy.mod[j] - moy)/et * sqrt(n.mod[j])/sqrt((sum(n.mod) - n.mod[j])/(sum(n.mod) - 1)) p.value = pnorm(abs(v.test), lower.tail = FALSE) * 2 if (!is.na(v.test)) { if (abs(v.test) > -qnorm(proba/2)) { result[[j]] = rbind(result[[j]], c(v.test, moy.mod[j], moy, sd.mod[j], et, p.value)) nom[[j]] = c(nom[[j]], colnames(donnee)[quanti[i]]) } } } } for (j in 1:nb.modalite) { if (!is.null(result[[j]])) { oo = rev(order(result[[j]][, 1])) result[[j]] = result[[j]][oo, ] nom[[j]] = nom[[j]][oo] if (nrow(matrix(result[[j]], ncol = 6)) > 1) { rownames(result[[j]]) = nom[[j]] colnames(result[[j]]) = c("v.test", "Mean in category", "Overall mean", "sd in category", "Overall sd", "p.value") } else { result[[j]] = matrix(result[[j]], ncol = 6) rownames(result[[j]]) = nom[[j]] colnames(result[[j]]) = c("v.test", "Mean in category", "Overall mean", "sd in category", "Overall sd", "p.value") } } } res$quanti = result } options(old.warn) class(res) <- c("catdes", "list ") return(res) } |
Utilisation :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
M <- read.csv("data_complete_with_groups.csv", header = TRUE, sep = ",") vars <- c(3:5, 12, 24:27, 45) # liste des numéros de colonnes correspondant aux variables utilisées pour la typo ET à la variable "groupe" X <- M[, vars] D <- apply(X, 2, as.factor) donnees <- as.data.frame(D) num.var <- 9 # la variable "groupe" est située en 9ème colonne de "donnees" proba = 0.05 # seuil de significativité = 5% weight <- M[, 2] # le poids des individus est en 2ème colonne de M source("catdes_w.R") # va permettre d'indiquer à R où trouver le code de la fonction "catdes.w" qu'on aura au préalable sauvegardée dans une fichier nommé "catdes_w.R" results <- catdes.w(donnees, num.var, proba = 0.05 , weight) G1 <- results$category$"1" G2 <- results$category$"2" G3 <- results$category$"3" G4 <- results$category$"4" G5 <- results$category$"5" K <- rbind(rep("",5), round(G1,3), rep("",5), rep("",5), round(G2,3), rep("",5), rep("",5), round(G3,3), rep("",5), rep("",5), round(G4,3), rep("",5), rep("",5), round(G5,3), rep("",5)) write.csv(K, file = "Typo1_5groups_weighted.csv", quote = FALSE) # va sauvegarder la description des groupes typo dans un fichier csv (qu'on pourra mettre en page par la suite, notamment en remplaçant les valeurs de type "q1_1=1" par le libellé correspondant) |
- Lecture des résultats -
Exemple de description d’un groupe :
| Cla / Mod | Mod / Cla | Global | p.value | v.test | |
|---|---|---|---|---|---|
| Q18 – Satisfaction : Clarté de la présentation = ST Pas satisfait | 71.43 | 78.43 | 13.93 | 3.70 10^-20 | 11.72 |
> Cla / Mod = 71,43 : 71,43 % des individus (parmis l’ensemble de la population à qui est posée cette question) qui sont « Non Satisfaits » par « la clarté de la présentation des informations » se retrouvent dans ce groupe.
> Mod / Cla = 78,43 et Global = 13,93 : dans ce groupe il y a 78,43 % des individus qui sont « Non Satisfaits » par « la clarté de la présentation des informations » alors que dans la population global il n’y en a que 13,93 %, il y a donc une sur-représentation de cette modalité dans le groupe.
> p.value = 3.70 10^-20 : La sur-représentation dans ce groupe de la modalité « Non Satisfaits » pour « la clarté de la présentation des informations » est significative au seuil 3.70×10^-20.
> v.test = 11.72 : valeur de la statistique de test permettant de déterminer la significativité des variables de description du groupe (si la valeur est positive, on aura une sur-représentation de la modalité considérée, si elle est négative, une sous-représentation).
C’est cette description de chacun des différents groupes qui va permettre ensuite de classer nos répondants dans des catégories bien spécifiques auxquelles on pourra donner des noms en rapport avec la description obtenue (par exemple « Les insatisfaits »).